18 Mart 2019 Pazartesi

3.ÜNİTE:DENKLEM VE EŞİTSİZLİKLER

SAYI KÜMELERİ
Sayma Sayıları \displaystyle \left( {{N}^{+}} \right)
\displaystyle \left( {{N}^{+}} \right) = {1, 2, 3,…}
kümesinin elemanlarının her biri birer sayma sayısıdır.
Doğal Sayılar (N)
Sıfır ve sayma sayılarının oluşturduğu sayı kümesine doğal sayılar kümesi denir. N ile gösterilir.
✓ N = {0, 1, 2, 3,…}
Örnek:
İlk 20 doğal sayının çarpımı kaçtır?
Çözüm
Doğal sayılar sıfırdan başladığından ilk 20 doğal sayı
{0, 1, 2, 3, 4, 5,…, 19} şeklindedir.
0.1.2.3.4…..19 = 0
Örnek:
a ve b birer doğal sayıdır a + b = 18 olduğuna göre a . b çarpımının alabileceği en büyük ve en küçük değerlerin toplamı kaçtır?
Çözüm
a ve b iki doğal sayı olduğuna göre;
a = 0 için, a + b = 18
0 + b = 18
a = 0 b = 18
a.b = 0
a=1 için a + b = 18
1 + b = 18
a = 1 b = 17
a.b = 17
a=2 için a + b = 18
2 + b = 18
a = 2 b = 16
a.b = 2.16 = 32
işlemlerini yaparak a ve b nin alabileceği tüm değerler için “a . b” çarpımını incelendiğinde
a + b = 18
0 + 18 ⇒ a.b = 0
1 + 17 ⇒ a.b = 17
2 + 16 ⇒ a.b = 32
3 + 15 ⇒ a.b = 45
…
9 + 9 ⇒ a.b = 81
değerleri bulunur. Buna göre a . b çarpımının en küçük değeri “0” ve en büyük değeri 81 dir. Bu değerlerin toplamı
0 + 81 = 81
Pozitif Tam Sayılar 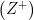\displaystyle \left( {{Z}^{+}} \right)
Sıfırdan büyük tam sayılara pozitif tam sayılar denir. 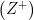\displaystyle \left( {{Z}^{+}} \right) sembolü ile gösterilir.
(+11, +40 gibi)
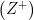✓ \displaystyle \left( {{Z}^{+}} \right) = {1, 2, 3, …}
pozitif-tam-sayilar
Negatif Tam Sayılar 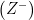\displaystyle \left( {{Z}^{-}} \right)
Sıfırdan küçük tam sayılara negatif tam sayılar denir. 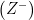\displaystyle \left( {{Z}^{-}} \right) sembolü ile gösterilir.
(-7, -13 gibi)
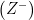✓ \displaystyle \left( {{Z}^{-}} \right) = {…, -3, -2,-1}
negatif-tam-sayilar
Tam Sayılar (Z)
Negatif tam sayılar, sıfır ve pozitif tam sayıların birleşmesi ile tam sayılar oluşur. “0” sayısı pozitif veya negatif değildir, nötrdür.
✓ Z = {…,-3,-2,-1, 0, 1, 2, 3, …}
Örnek:
a ve b birer tam sayı olmak üzere a . b = 40 olduğuna göre “a + b” ifadesinin en büyük değeri ile en küçük değeri arasındaki fark kaçtır?
Çözüm
a ve b birer tam sayı a . b = 40
a . b ifadesinin en büyük değerini hesaplamak için a ve b nin pozitif değer seçilmesi gerekir.
a . b = 40 kabulüne göre a + b ifadesini incelersek
40 . 1 = 40 ⇒ a + b = 40 + 1 = 41
20 . 2 = 40 ⇒ a + b = 20 + 2 = 22
10 . 4 = 40 ⇒ a + b = 10 + 4 = 14
8 . 5 = 40 ⇒ a + b = 8 + 5 = 13
görüldüğü gibi ifadenin en büyük değeri; 41 dir.
a + b ifadesinin en küçük değeri için a ve b nin negatif seçilmesi gerekir.
a . b = 40 kabulüne göre a + b ifadesini incelersek
(-40) . (-1) = 40 ⇒ a + b = (-40) + (-1) = -41
(-20) . (-2) = 40 ⇒ a + b = (-20) + (-2) = -22
(-10) .(-40) = 40 ⇒ a + b = (-10) + (-4) = -14
(-8) . (-5) = 40 ⇒ a + b = (-8) + (-5) = -13
görüldüğü gibi ifadenin en küçük değeri -41 dir.
a + b ifadesinin en büyük değeri ile en küçük değeri arasındaki farkı hesaplarsak aşağıdaki sonucu elde ederiz.
41- (-41) = 82
Rasyonel Sayılar (Q)
Paydası 0 dan farklı olmak üzere \displaystyle \frac{a}{b} şeklinde yazılabilen sayılara rasyonel sayılar denir.
✓ \displaystyle Q=\left\{ \frac{a}{b}:a,b\in Z,b\ne 0 \right\}
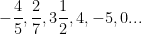✓ \displaystyle -\frac{4}{5},\frac{2}{7},3\frac{1}{2},4,-5,0... gibi
İrrasyonel Sayılar (I)
\displaystyle \sqrt{2},\sqrt{3},\pi  gibi tam değeri belli olmayan diğer bir deyişle virgülden sonraki kısmı hesaplanmayacak kadar büyük olan sayılardır.
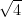✓ \displaystyle \sqrt{4} rasyoneldir. 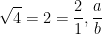\displaystyle \sqrt{4}=2=\frac{2}{1},\frac{a}{b} şeklinde yazılabiliyor.
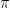✓ \displaystyle \pi  irrasyoneldir. 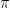\displaystyle \pi  = 3,141592653589793238462643383279502…
Reel Sayılar (R)
Rasyonel ve irrasyonel sayıların birleşmesiyle oluşan bütün sayılar reel sayılar kümesini oluşturur.
✓ \displaystyle R=Q\cup I
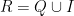
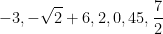✓ \displaystyle -3,-\sqrt{2}+6,2,0,45,\frac{7}{2} gibi sayıların hepsi reel sayılardır.



2.BÖLME VE BÖLÜNEBİLME KURALLARI








A. BÖLME
A, B, C, K birer doğal sayı ve B ¹ 0 olmak üzere,
      
bölme işleminde,
  • A ya bölünen, B ye bölen, C ye bölüm, K ya kalan denir.
  • A = B × C + K dir.
  • Kalan, bölenden küçüktür. (K < B)
  • Kalan, bölümden (C den) küçük ise, bölen (B) ile bölümün (C) yeri değiştirilebilir. Bu durumda A ve K değişmez.
  • K = 0 ise, A sayısı B ile tam bölünebilir.

B. BÖLÜNEBİLME KURALLARI
1. 2 İle Bölünebilme
Birler basamağındaki rakamı çift olan sayılar 2 ile tam bölünür.
Tek sayıların 2 ile bölümünden kalan 1 dir.
2. 3 İle Bölünebilme
Rakamlarının sayısal değerleri toplamı 3 ün katı olan sayılar 3 ile tam bölünür.
Bir sayının 3 ile bölümünden kalan, rakamlarının toplamının 3 ile bölümünden kalana eşittir.
3. 4 İle Bölünebilme
Bir sayının onlar basamağındaki rakam ile birler basamağındaki rakamın (son iki basamak) belirttiği sayı, 4 ün katı olan sayılar 4 ile tam bölünür.
... abc sayısının 4 ile bölümünden kalan bc nin (son iki basamak) 4 ile bölümünden kalana eşittir.
  • ... abc sayısının 4 ile bölümünden kalan
c + 2 . b nin 4 ile bölümünden kalana eşittir.
4. 5 İle Bölünebilme
Birler basamağındaki rakam 0 veya 5 olan sayılar 5 ile tam bölünür.
Bir sayının 5 ile bölümünden kalan, o sayının birler basamağındaki rakamın 5 ile bölümünden kalana eşittir.
5. 7 İle Bölünebilme
(n + 1) basamaklı anan-1 ... a4a3a2a1a0 sayısının 7 ile tam bölünebilmesi için,
k eleman Z olmak üzere,
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) +...– ... = 7k
olmalıdır.
Ü
Birler basamağı a0, onlar basamağı a1, yüzler basamağı a2, ... olan sayının (...a5 a4 a3 a2 a1 a0sayısının) 7 ile bölümünden kalan
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) +...– ... ...
işleminin sonucunun 7 ile bölümünden kalana eşittir.
Sekiz basamaklı ABCDEFGH sayısının 7 ile bölümünden kalan,
(H + 3 × G + 2 × F) – (E + 3 × D + 2 × C) + (B + 3 × A) işleminin sonucunun 7 ile bölümünden kalandır.
6. 8 İle Bölünebilme
Yüzler basamağındaki, onlar basamağındaki ve birler basamağındaki rakamların (son üç rakamın) belirttiği sayı 8 in katı olan sayılar 8 ile tam bölünür.
3000, 3432, 65104 sayıları 8 ile tam bölünür.
Ü
Birler basamağı c, onlar basamağı b, yüzler basamağı a, ... olan sayının (... abc sayısının) 8 ile bölümünden kalan c + 2 × b + 4 × a toplamının 8 ile bölümünden kalana eşittir.
7. 9 İle Bölünebilme
Rakamlarının toplamı 9 un katı olan sayılar 9 ile tam bölünür.
Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalana eşittir.
8. 10 İle Bölünebilme
Birler basamağındaki rakamı 0 (sıfır) olan sayılar 10 ile tam bölünebilir. Bir sayının birler basamağındaki rakam o sayının 10 ile bölümünden kalandır.
9. 11 İle Bölünebilme
(n + 1) basamaklı anan–1 ... a4a3a2a1a0 sayısının 11 ile tam bölünebilmesi için
(a0 + a2 + a4 + ...) – (a1 + a3 + a5 + ...)... = 11 . k
ve (k eleman Z) olmalıdır.
Ü
(n + 1) basamaklı anan–1 ... a4a3a2a1a0 sayısının 11 ile bölümünden kalan
(a0 + a2 + a4 + ...) – (a1 + a3 + a5 + ...)... işleminin sonucunun 11 ile bölümünden kalana eşittir.
Aralarında asal iki sayıya bölünebilen bir sayı, bu iki sayının çarpımına da tam bölünür.
  • 2 ve 3 ile tam bölünen sayılar 2 × 3 = 6 ile de tam bölünür.
  • 3 ve 4 ile tam bölünen sayılar 3 × 4 = 12 ile de tam bölünür.
  • 4 ve 6 ile tam bölünen sayılar 4 × 6 = 24 ile tam bölünemeyebilir. Çünkü 4 ile 6 aralarında asal değildir.
C. BÖLEN KALAN İLİŞKİSİ
A, B, C, D, E, K1, K2 uygun koşullarda birer doğal sayı olmak üzere,
A nın C ile bölümünden kalan K1 ve
B nin C ile bölümünden kalan K2 olsun.
Buna göre,
  • A × B nin C ile bölümünden kalan K1 × K2 dir.
  • A + B nin C ile bölümünden kalan K1 + K2 dir.
  • A – B nin C ile bölümünden kalan K1 – K2 dir.
  • D × A nın C ile bölümünden kalan D × K1 dir.
  • AE nin C ile bölümünden kalan (K1)E dir.
Yukarıdaki işlemlerde kalan değerler bölenden (C den) büyük ise, tekrar C ile bölünerek kalan bulunur.
D. ÇARPANLAR İLE BÖLÜM
Bir A doğal sayısı B × C ile tam bölünüyorsa A sayısı B ve C doğal sayılarıyla da bölünebilir. Fakat bu ifadenin karşıtı (A sayısı B ile ve C ile tam bölünüyorsa A sayısı B × C ile tam bölünür.) doğru olmayabilir.
  • 144 sayısı 2 × 6 = 12 ile tam bölünür ve 144 sayısı 2 ile ve 6 ile de tam bölünür.
  • 6 sayısı 2 ile ve 6 ile tam bölünür. Fakat 6 sayısı 2 × 6 = 12 ile tam bölünemez.
E. BİR TAM SAYININ TAM BÖLENLERİ
Bir tam sayının, asal çarpanlarının kuvvetlerinin çarpımı biçiminde yazılmasına bu sayının asal çarpanlarının kuvvetleri biçiminde yazılması denir.
a, b, c birbirinden farklı asal sayılar ve m, n, k pozitif tam sayılar olmak üzere,
A = am . bn . ck  olsun.
Bu durumda aşağıdakileri söyleyebiliriz:
  • A yı tam bölen asal sayılar a, b, c dir.
  • A sayısının pozitif tam bölenlerinin sayısı,
      (m + 1) × (n + 1) × (k + 1) dir.
  • A sayısının pozitif tam bölenlerinin ters işaretlileri de negatif tam bölenidir.
  • A sayısının tam sayı bölenleri sayısı,
          2 × (m + 1) × (n + 1) × (k + 1) dir.
  • A sayısının tam sayı bölenleri toplamı 0 (sıfır) dır.
  • A sayısının pozitif tam bölenlerinin toplamı,
          
  • A sayısının asal olmayan tam sayı bölenlerinin sayısı, A nın tam sayı bölenlerinin sayısından A nın asal bölenlerinin sayısı çıkarılarak bulunur.
  • A nın asal olmayan tam sayı bölenleri toplamı,
          – (a + b + c) dir.
  • A sayısından küçük A ile aralarında asal olan doğal sayıların sayısı,
          
  • A sayısının pozitif tam sayı bölenlerinin çarpımı:
      



BİRİNCİ DERECEDEN DENKLEMLER VE EŞİTSİZLİKLER


PDF NOTUNA ULAŞMAK İÇİN TIKLA:
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
Bu ders notumuzda YGS, KPSS, DGS, SBS ve daha bir çok sınavda karşımıza çıkan Birinci Dereceden Denklemler konusunun geniş konu anlatımını, konun önemli yerlerini bulabilirsiniz.
A. TANIM
a ve b gerçel (reel) sayılar ve a ¹ 0 olmak üzere,
ax + b = 0 eşitliğine birinci dereceden bir bilinmeyenli denklem denir.
Bu denklemi sağlayan x değerlerine denklemin kökü, denklemin kökünün oluşturduğu kümeye denklemin çözüm kümesi denir.
B. EŞİTLİĞİN ÖZELİKLERİ
 Denklem çözümünde aşağıdaki özeliklerden yararlanırız.
  1. Bir eşitliğin her iki tarafına aynı sayı ilave edilirse eşitlik bozulmaz.
A = B İSE, A + C = B + C DİR.
  1. Bir eşitliğin her iki tarafından aynı sayı çıkarılırsa eşitlik bozulmaz.
A = B İSE, A – C = B – C DİR.
  1. Bir eşitliğin her iki tarafı aynı sayı ile çarpılırsa eşitlik bozulmaz.
A = B İSE, A × C = B × C DİR.
  1. Bir eşitliğin her iki tarafı sıfırdan farklı aynı sayı ile bölünürse eşitlik bozulmaz.derscalisiyorum.com.tr

  1. Bir eşitliğin her iki tarafının n. kuvveti alınırsa eşitlik bozulmaz.
A = B İSE, AN = BN DİR.
  1. derscalisiyorum.com.tr
  2. (a = b ve b = c) ise, a = c dir.
  3. (a = b ve c = d) ise, a ± c = b ± d dir.
  4. (a = b ve c = d) ise, a × c = b × d dir.
  5. derscalisiyorum.com.tra × b = 0 ise, (a = 0 veya b = 0) dır.
  6. a × b ¹ 0 ise, (a ¹ 0 ve b ¹ 0) dır.
  7. derscalisiyorum.com.tr

C. ax + b = 0 DENKLEMİNİN ÇÖZÜM KÜMESİ
  1. a ¹ 0 olmak üzere,derscalisiyorum.com.tr

  1. (a = 0 ve b = 0) ise, ax + b = 0 denklemini bütün sayılar sağlar. Buna göre, reel (gerçel) sayılarda çözüm kümesi derscalisiyorum.com.trdir.
  2. (a = 0 ve b ¹ 0) ise, ax + b = 0 denklemini sağlayan hiçbir sayı yoktur. Yani, Ç = Æ dir.

D. BİRİNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEM SİSTEMİa, b, c Îderscalisiyorum.com.tr, a ¹ 0 ve b ¹ 0 olmak üzere,
ax + by + c = 0 denklemine birinci dereceden iki bilinmeyenli denklem denir.
Bu denklem düzlemde bir doğru belirtir. Doğru üzerindeki bütün noktaların oluşturduğu ikililer denklemin çözüm kümesidir.
Buna göre, ax + by + c = 0 denkleminin çözüm kümesi birçok ikiliden oluşur.
a, b, c Πderscalisiyorum.com.trolmak üzere,ax + by + c = 0denklemi her (x, y) Îderscalisiyorum.com.tr2 için sağlanıyorsaa = b = c = 0 dır.

Birden fazla iki bilinmeyenli denklemden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin BulunmasıBirinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi; yok etme yöntemi, yerine koyma yöntemi, karşılaştırma yöntemi, grafik yöntemi, determinant yöntemi gibi yöntemlerden biri ile yapılır.
Biz burada üçünü vereceğiz.
a. Yok Etme Yöntemi: Değişkenlerden biri yok edilecek biçimde verilen denklem sistemi düzenlenir ve taraf tarafa toplanır.
Taraf tarafa toplandığında veya çıkarıldığında (ya da bir düzenlemeden sonra) değişkenlerden biri sadeleşiyorsa “Yok etme yöntemi” kolaylık sağlar.

b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, değişkenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
Denklemlerin birinden, değişkenlerden biri kolayca çekilebiliyorsa, “Yerine koyma yöntemi” kolaylık sağlar.

c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişken çekilir. Denklemlerin diğer tarafları karşılaştırılır (eşitlenir).
Her iki denklemden de aynı değişken kolayca çekilebiliyorsa, “Karşılaştırma yöntemi”kolaylık sağlar.

Üax + by + c = 0dx + ey + f = 0
denklem sistemini göz önüne alalım:
Bu iki denklemin her birinin düzlemde bir doğru belirttiği göz önüne alınırsa üç durumolduğu görülür.
AX + BY + C = 0
DX + EY + F = 0
denklem sisteminde,ise, bu iki doğru tek bir noktada kesişir.
Birinci durum:
derscalisiyorum.com.tr
Bu durumda, verilen denklem sisteminin çözüm kümesi bir tek noktadan oluşur.
İkinci durum:ise, bu iki doğru çakışıktır.
derscalisiyorum.com.tr
Doğru üzerindeki her nokta denklem sistemini sağlar.
Bu durumda, verilen denklem sisteminin çözüm kümesi sonsuz noktadan oluşur.
Üçüncü durum:ise, bu iki doğru paraleldir.
derscalisiyorum.com.tr
Denklem sistemini sağlayan hiçbir nokta bulunamaz.
Bu durumda, verilen denklem sisteminin çözüm kümesi boş kümedir.
Birinci Dereceden bir bilinmeyenli basit eşitsizlikler konusu 9. sınıf matematik müfredatında gerçek sayılar ve denklemler ünitesi içerisinde yer almaktadır. Bu yazımızda Birinci Dereceden bir bilinmeyenli eşitsizlikler konu anlatımı ve soru çözümleri videoları ile ders notlarını bulabilirsiniz. Konu içerisinde farklı öğretmenlere ait ders videoları paylaşılmıştır. Aynı konuyu farklı öğretmenlerden dinleyerek konuyu daha iyi pekiştirebilirsiniz.

Eşitsizlik Nedir?

Bir niceliğin diğer bir nicelikten büyük veya küçük olma durumunu belirten ifadelere ise eşitsizlikdenir. Eşitsizliklerin ifade edilmesinde >, ≥, <, ≤ sembolleri kullanılır.
ax + b > 0 , ax + b ≥ 0 , ax + b < 0 , ax + b ≤ 0 şeklinde ifade edilebilen eşitsizliklere birinci dereceden bir bilinmeyenli eşitsizlikler denir. 2x – 3 > 5 , x – 2 < 0 , 25 – a ≤ 3a ifadeleri birinci dereceden bir bilinmeyenli eşitsizliklere birer örnektir. Denklemler ve eşitsizlikler, gerçek hayat durumlarının matematiksel olarak ifade edilmesinde ve incelenmesinde kullanılır.

Bir denklemde/eşitsizlikte değişkenin bazı değerleri eşitliği/eşitsizliği sağlayabilirken bazıları sağlamayabilir. Denklemi/eşitsizliği sağlayan sayıların kümesine o denklemin/eşitsizliğin çözüm kümesi denir.


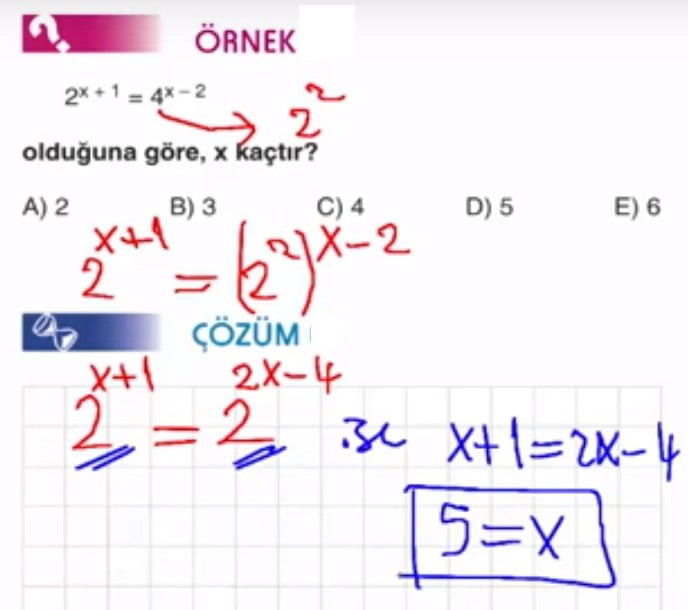
ÜSLÜ İFADELER VE DENKLEMLER

 

 Üslü İfadenin Tanımı: n pozitif tam sayı ve a gerçek sayı olmak üzere, a sayısının kendisiyle n defa çarpılmasına a nın n inci kuvveti denir ve an biçiminde yazılır.
an ifadesine üslü sayı, a ya taban, n ye de üs veya kuvvet denir.

Üslü Sayıların Özellikleri

Üslü Denklemler

Üslü Eşitsizlikler

Üslü İfade ve Denklemler Çözümlü Sorular








-

Hiç yorum yok:

Yorum Gönder

Kaydol: Kayıt Yorumları (Atom)

9.SINIF PDF MATEMATİK

9.SINIF PDF MATEMATİK İSTERSENİZ TÜM KONULARI İÇEREN 9.SINIF PDF MATEMATİK KİTABINI AŞAĞIDAKİ LİNKTEN SATIN ALARAK MATEMATİK ÇALIŞABİLİR...

  • (başlık yok)
    4.ÜNİTE:ÜÇGENLER ÜÇGENLERDE TEMEL KAVRAMLAR Açı Çeşitleri Açı Çeşitleri Çözümlü Örne...
  • (başlık yok)
    1.ÜNİTE: MANTIK ÖNERMELER VE BİLEŞİK ÖNERMELER Mantık Nedir? Mantık, doğru düşünme biçimini araştıran bir araştırma alanıd...
  • (başlık yok)
    3.ÜNİTE: DENKLEM VE EŞİTSİZLİKLER SAYI KÜMELERİ Sayma Sayıları   = {1, 2, 3,…} kümesinin elemanlarının her biri birer sayma say...