2.ÜNİTE:KÜMELER


KÜMELERDE TEMEL KAVRAMLAR

A) KÜME KAVRAMI ve KÜMELERİN GÖSTERİMİ
a) Küme Kavramı
Küme, nesnelerin özelliklerine göre tanımlanmış bir topluluktur.

Kümeyi oluşturan nesnelerin her birine kümenin elemanları denir.

Kümeler genellikle A, B, C, D, K, ... gibi büyük harflerle gösterilir.

Bir a elemanı C kümesinin elemanı ise bu durum “a ∈ C” biçiminde yazılır ve
“a elemanıdır C” diye okunur.

Bir b elemanı F kümesinin elemanı değilse bu durum “b ∉ F” biçiminde yazılır ve
“b elemanı değildir F” diye okunur.

Bir A kümesinin eleman sayısı s(A) ile gösterilir.

!!! Kümede, aynı eleman bir defa yazılır.

b) Liste Yöntemi
Kümenin elemanlarının, { } biçimindeki bir parantez içine sıra gözetilmeden yazılmasına “liste yöntemiyle gösterme” denir.
A = {1, 3, 5, 7}

c) Ortak Özellik Yöntemi
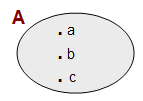
Kümenin elemanlarının ortak özelliklerinin belirtilerek yazılmasına “ortak özellik yöntemi” denir.
A = {20 den küçük çift doğal sayılar}

d) Venn Şeması
Kümeyi oluşturan elemanların kapalı bir şekil içine, önüne “•” konularak yazılmasına “Venn Şeması” ile gösterim denir.

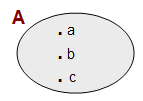
B) KÜMELERİN ÇEŞİTLERİ
a) Evrensel Küme
Üzerinde işlem yapılan bütün kümeleri kapsayan, boş kümeden farklı olan kümeye evrensel küme denir. Genellikle E harfi ile gösterilir.

b) Sonlu Küme
Elemanları sayılarak bitirilebilen kümelere sonlu küme denir.
A = {7 ile 26 arasındaki doğal sayılar}

c) Sonsuz Küme
Elemanları sayılarak bitirilemeyen kümelere sonsuz küme denir.
A = {36 dan büyük doğal sayılar}

d) Boş Küme
Elemanı olmayan kümeye boş küme denir. Boş küme {} ya da Ø sembolü ile gösterilir.
A = {}
B = {Haftanın üç harfli günleri}

C) ALT KÜME
a) Alt Küme
A ve B herhangi iki küme olsun.
B kümesinin her elemanı A kümesininde elemanı ise, B ye A kümesinin alt kümesi denir ve B ⊂ A biçiminde gösterilir.

B kümesi A kümesinin alt kümesi ise, A kümesi B kümesini kapsar denir ve
A ⊃ B biçiminde gösterilir.

ÖNEMLİ
* Boş küme her kümenin alt kümesidir. (Ø ⊂ A)

* Her küme kendisinin alt kümesidir. (A ⊂ A)

* Her küme evrensel kümenin alt kümesidir. (A ⊂ E)

* A, B ve C kümeleri verilsin. (A ⊂ B) ve (B ⊂ C) ise A ⊂ C dir.

* A ve B kümeleri verilsin. (A ⊂ B) ve (B ⊂ A) ⇔ A = B dir.

* s(A) = n olmak üzere,
• A kümesinin alt küme sayısı; 2ⁿ dir.

• A kümesinin r elemanlı alt kümelerin sayısı;• A kümesinin en çok r elemanlı alt kümelerinin sayısı;• A kümesinin en az r elemanlı alt kümelerinin sayısı;

b) Özalt Küme
Bir kümenin, kendisi hariç diğer alt kümelerine o kümenin özalt kümeleri denir. s(A) = n olmak üzere, A kümesinin özalt kümelerinin sayısı 2ⁿ – 1 dir.

c) Kuvvet Kümesi
Bir kümenin alt kümelerinin kümesine kümenin kuvvet kümesi denir. A kümesinin kuvvet kümesi P(A) ile gösterilir.

D) EŞİT KÜMELER
Eşit Küme
Aynı elemanlardan oluşan kümelere eşit kümeler denir.
A kümesinin B kümesine eşitliği A = B biçiminde gösterilir.

KÜMELERDE  İŞLEMLER

Kümelerle İşlemler

.

Birleşim İşlemi
İki kümenin bütün elemanlarından oluşan kümeye iki kümenin birleşimi denir. A ve B kümelerinin birleşimi “AuB” biçiminde gösterilir ve “A birleşim B” diye okunur.
Örnek

AuB = {1, 2, 3, 4, a, b}’dir.

.

Kesişim İşlemi
iki kümede bulanan ortak elemanlardan oluşan kümeye iki kümenin kesişimi denir. A ve B kümelerinin kesişimi “AnB” biçiminde gösterilir ve “A kesişim B” diye okunur.
Örnek

AnB = {a, b}’dir.

.

Fark İşlemi
A kümesinin elemanı olup B kümesinin elemanı olmayan elamanlardan oluşan kümeye A fark B kümesi denir. “AB” biçiminde gösterilir ve “A fark B” diye okunur.
Örnek

AB = {1, 2}’dir. BA = {3, 4}’tür.

Bir Kümenin Tümleyeni
E kümesinin elemanı olup A kümesinin elemanı olmayan elemanlardan oluşan kümeye A kümesinin tümleyeni denir. “AI” biçiminde gösterilir ve “A’nın tümleyeni” diye okunur.

E A = AI

.

Örnek

E = {a, b, c, d}
A = {a, b}
EA = AI = {c, d}’dir.

sevgili arkadaşlar 9.sınıf kümelerde temel kavramlar ve kümelerde işlemler konu anlatımımızın sonuna geldik. bir sonraki 9.sınıf matematik dersimizde görüşmek dileğiyle

KATEGORİLER